首页 数字图像处理学习笔记5
文章
取消

数字图像处理学习笔记5

发表于 2022/11/19 更新于 2022/11/21
作者 HuangHongxing
14 分钟阅读

把图像空间按照一定的要求分成一些“有意义”的区域的技术称为图像分割。 图像分割基本原理：图像亮度值 ==> （区域之间）不连续性；（区域内部）相似性。 不连续性： 不同区域交界、边缘处像素灰度值具有不连续突变性。 相似性： 同一区域内像素一般具有灰度相似性，据此找到灰度值相似的区域，区域的外轮廓就是对象的边缘。

一、点、线和边缘检测（检测图像中的点、线和边缘）

1. 点检测（使用滤波器）

点的定义：图像的一个区域，亮度几乎不变。 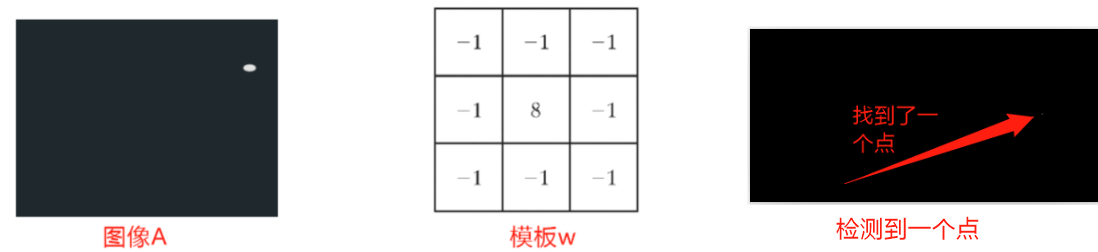f7a464b8717957fd18cd624887802ee2.png 当模板刚好套在图像A中的点时，该点响应最大，以此来发现这里有一个点。因为其他区域的像素值都0，模板在这些像素的响应值都是0（线性滤波器）；

1
2
3
4
5
6
7
8
9
10

f = im2double(rgb2gray(imread('dot.jpg'))); % imfilter的输入图像和输出图像的数据类型一致，
w = [-1 -1 -1; -1 8 -1; -1 -1 -1];  % 但运算时按float进行运算，故而使用im2double保证不丢失数据。
g = abs(imfilter(f, w)); % 图像g的每个像素值都是f对应像素点的响应值，里面最大的像素值的位置就有一个点
T = max(g(:)); % 找到图像g中最大的那个值
g = g >= T; % 位置筛选，图g只有两个值：0和1
imshow(g); % 值为1的像素显示白点
或者 
g = ordfilt2(f, m*n, ones(m, n)) − ordfilt2(f, 1, ones(m, n)); % 依据不连续性，点 的邻域极差大
g = g >= T; % 将极差大的像素点筛选出来
imshow(g);
2. 线检测

线检测模板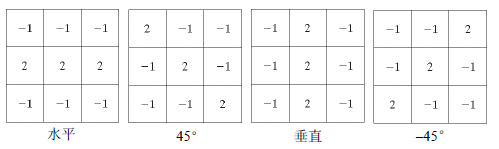：e8c8311bc9a5569e88ab76ef10f10337.png 过程和点检测一样。 使用霍夫（Hough）变换进行线检测： 之前的线检测方法只产生位于边缘上的像素，使用霍夫变换能将这些像素组装成有意义的边缘。 Hough变换基本原理：边界上有n个点，这些点构成点集，找到这个点集共线的子集及其对应的直线方程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

f = zeros(101, 101);
f(1, 1) = 1;f(101, 1) = 1; f(1, 101) = 1;
f(101, 101) = 1;f(51, 51) = 1;
for i = 25:75
    f(i, i) = 1;
end
subplot(231), imshow(f), title('原图');
[H, theta, rho] = hough(f);
subplot(232), imshow(H, 'XData', ...
    theta, 'YData', rho, 'InitialMagnification', 'fit');
title('霍夫空间（极坐标）');
axis on, axis normal; xlabel('\theta'), ylabel('\rho');
peaks = houghpeaks(H, 10);
hold on;
plot(theta(peaks(:, 2)), rho(peaks(:, 1)), ...
    'linestyle', 'none', 'marker', 's', 'color', 'g');
lines = houghlines(f, theta, rho, peaks);
subplot(233), imshow(f), title('边缘连线'), hold on;
for k = 1:length(lines)
    xy = [lines(k).point1; lines(k).point2];
    plot(xy(:, 1), xy(:, 2), 'LineWidth', 4, ...
        'Color', [.8 .8 .8]);
end

c722149a5e32485bdf3c716d01747b3a.png 25cc99bd4c725054eb73d50a5ede8222.png Matlab霍夫变换步骤：hough进行霍夫变换，将原图映射到霍夫空间里；houghpeaks在霍夫空间里求出峰值；houghlines检测是否有与峰值相关的有意义的的线段，如果有，找出这些线段。

3. 边缘检测（使用edge函数）

边缘检测算子： c72500a14d18ab1ef8de750b91577b73.png edge(f, '<method>', T, direction)：f是输入图像，’'是边缘检测算子，T是阈值，direction是检测边缘的首选方向：`'horizontal'`, `'vertical'`, '`both'(默认)` 。

二、阈值处理

使用阈值将图像按灰度值划分区域。

1. 全局阈值处理

要求：目标和背景的灰度差较大，直方图有明显谷底。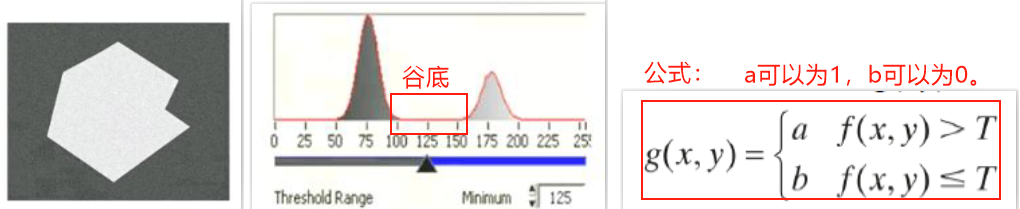4b6b990de7e17a9ebcdc60e589f31261.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# globalThreshold.m
function [T, count] = globalThreshold(f, threshold)
    if nargin == 1
        threshold = 0.5;
    end
    count = 0;
    T = mean2(f);
    done = false;
    while ~done
        count = count + 1;
        g = f > T;
        Tnext = 0.5 * (mean(f(g)) + mean(f(~g)));
        done = abs(T - Tnext) < threshold;
        T = Tnext;
    end
end
# main.m
f = rgb2gray(imread('test.jpg'));
[T, c] = globalThreshold(f);
g = imbinarize(f, T/255);
subplot(221), imshow(f);
subplot(222), imhist(f);
subplot(223), imshow(g);
subplot(224), histogram(f, 256);

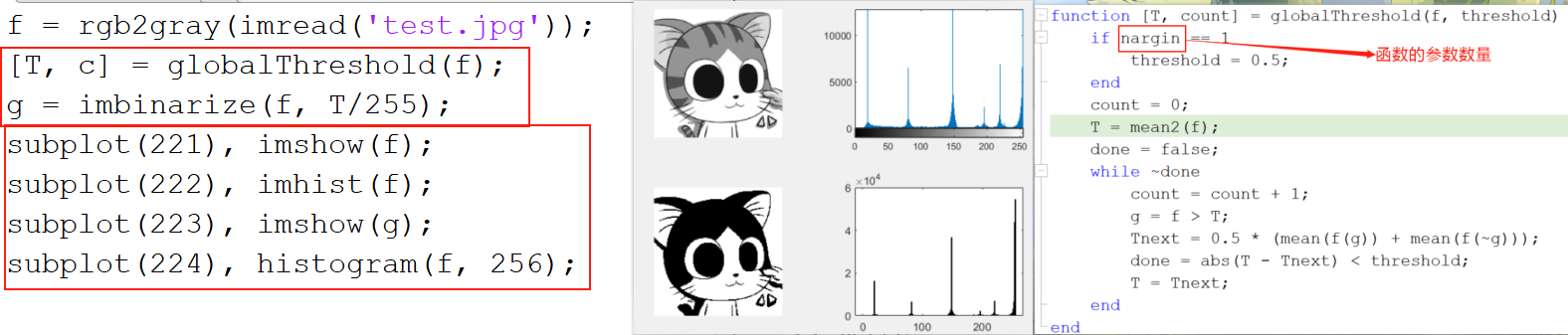
e6472b8c1a644537521a8c08de42cbb0.png imhist和histogram的区别：imhist的NumBins值是由图像类型决定的。若图像为uint8类型，则bin的数量为256，即[0:1:255]。histogram的NumBins值可以人为设定，在未指定该参数时，系统将基于图像的灰度分布自动计算NumBins的值。（bin是直条，NumBins是直条数量） OTSU算法（大津法、最大类间方差法）：

大津法（OTSU）是一种确定图像二值化分割阈值的算法。从大津法的原理上来讲，该方法又称作最大类间方差法，因为按照大津法求得的阈值进行图像二值化分割后，前景与背景图像的类间方差最大。 它被认为是图像分割中阈值选取的最佳算法，计算简单，不受图像亮度和对比度的影响，因此在数字图像处理上得到了广泛的应用。它是按图像的灰度特性，将图像分成背景和前景两部分。因方差是灰度分布均匀性的一种度量,背景和前景之间的类间方差越大,说明构成图像的两部分的差别越大,当部分前景错分为背景或部分背景错分为前景都会导致两部分差别变小。因此,使类间方差最大的分割意味着错分概率最小。 应用：是求图像全局阈值的最佳方法，应用不言而喻，适用于大部分需要求图像全局阈值的场合 优点：计算简单快速，不受图像亮度和对比度的影响。 缺点：对图像噪声敏感；只能针对单一目标分割；当目标和背景大小比例悬殊、类间方差函数可能呈现双峰或者多峰，这个时候效果不好。

Matlab用graythresh计算OTSU全局阈值（范围0~1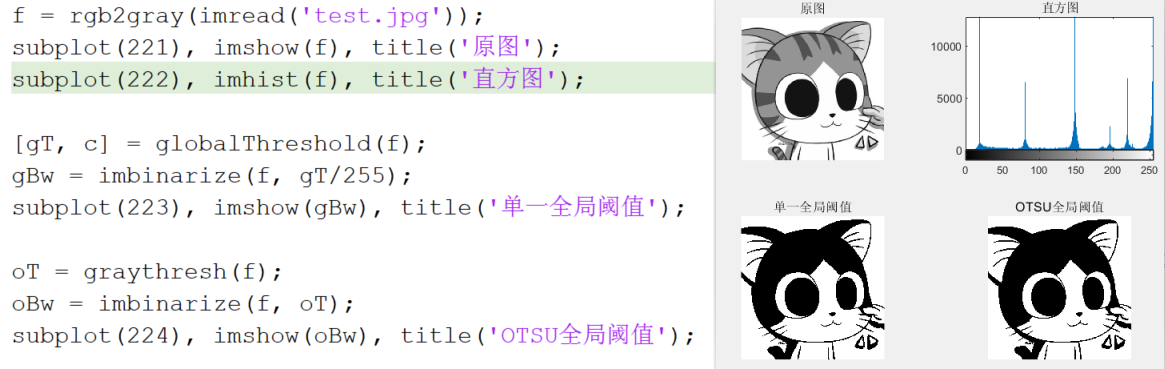）。 d8af4ee84e9f3b56f1ae33053b628573.png 图像平滑： 所谓平滑，其实就是如果原图中有噪声，要先利用滤波器进行去噪处理（平滑操作），然后再进行阈值处理。 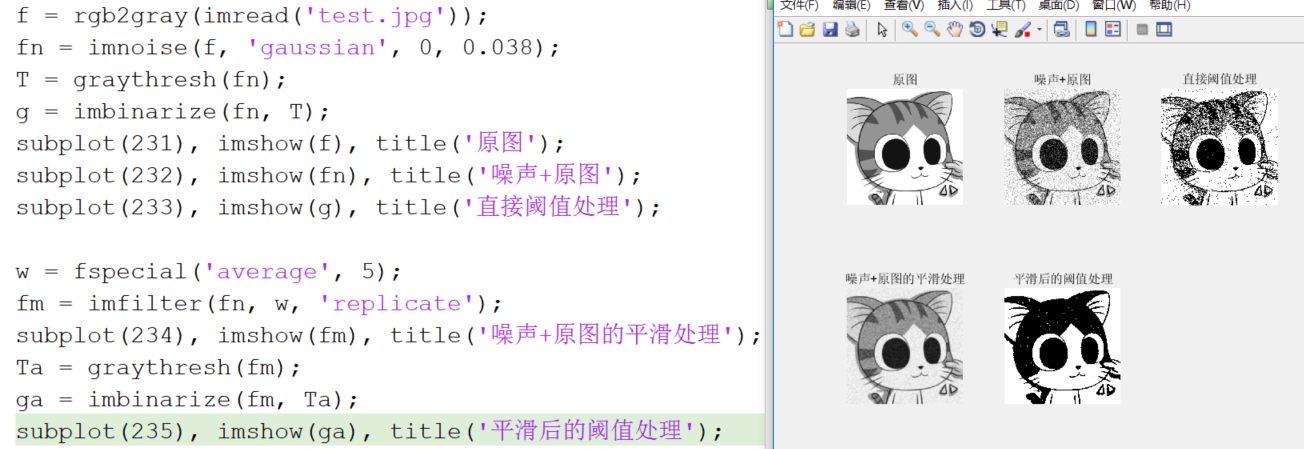4eedbdd82fd72b23065c0737c05f6023.png 使用边缘改进全局阈值处理： 对于边界明显的图像，但是整体灰度值相近，不易用otsu直接找出正确的阈值，可以使用边缘改进的阈值处理。其中，有基于梯度的边缘信息改进全局阈值处理和基于拉普拉斯边缘信息改进全局阈值处理。 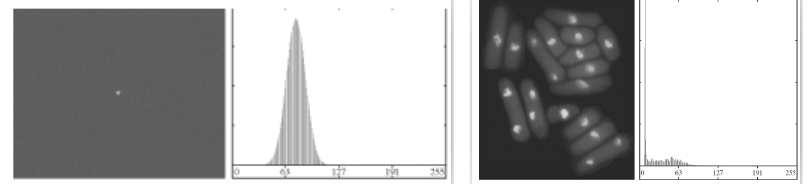8c5df72735b7ca347d14f46ec3fa47fa.png

2. 局部阈值处理

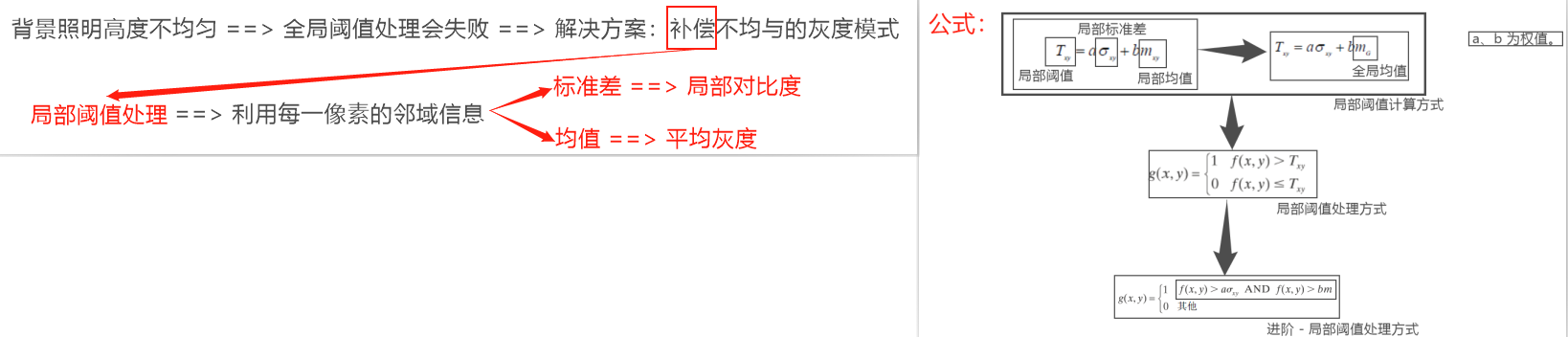
a4d644e6fd034b0128207b30727134a8.png 7f423e6659e1be439e31e149b35b7ea4.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

# localthresh.m 计算每个像素点的局部标准差和局部均值，然后加权相加，计算出局部阈值
function g = localthresh(f, nhood, a, b, meantype)
    # a, b 是分别是局部标准差和均值的权值，a变大 ==> 加大局部对比度，b变大 ==> 局部灰度值变高
    f = im2double(f);
    sig = stdfilt(f, nhood);
    if nargin == 5 && strcmp(meantype, 'global')
        mean = mean2(f);
    else
        mean = localmean(f, nhood);
    end
    g = (f > a * sig) & ( f > b * mean);
end
# localmean.m 使用均值滤波计算每个像素的局部均值
function mean = localmean(f, nhood)
    if nargin == 1
        nhood = ones(3) / 9;
    else 
        nhood = nhood / sum(nhood(:));
    end
    mean = imfilter(im2double(f), nhood, 'replicate');
end

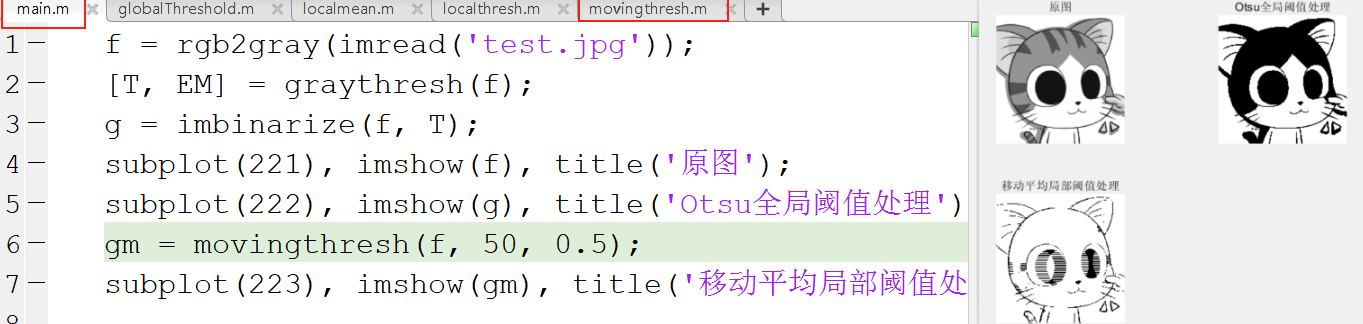
移动平均的局部阈值处理： 以一幅图像的扫描行计算移动平均为基础，能减少光照偏差。当感兴趣的物体与图像尺寸相比较小(或较细)时，该处理方法效果很好，譬如：打印图像和手写文本图像。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

# movingthresh.m
function g = movingthresh(f, n, K)
    f = im2double(f);
    [M, N] = size(f);
    if (n < 1) || (rem(n, 1) ~= 0)
        error('n必须是大于1的整数。')
    end
    if K < 0 || K > 1
        error('K必须是在0~1的小数。')
    end
    f(2:2:end, :) = fliplr(f(2:2:end, :));
    f = f'; 	
    f = f(:)';
    maf = ones(1, n)/n; 	
    ma = filter(maf, 1, f);
    g = f > K * ma;
    g = reshape(g, N, M)';
    g(2:2:end, :) = fliplr(g(2:2:end, :));
end

29f5e3fb31986ef1e7a9c81a37292092.png

三、基于区域的分割

原理：寻找区域。 区域：自己定义一个准则（如灰度级相似），在这个准则内的像素处于同一区域。 分为两类：区域生长法，区域分裂与合并。

1. 区域生长法

原理：根据一定的相似度准则将像素或子区域聚合成更大的区域。 相似度准则：灰度级相似，纹理相似，颜色相似。 灰度级相似准则：某点像素a，如果发现a邻域里有个像素b的值和它差不多（abs(a-b) < 阈值），则将a和b归为同一区域。 abd7e453eb69badcc7840a2310e707ce.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

# regiongrow.m 灰度级相似准则
function [g, NR, SI, TI] = regiongrow(f, S, T)
    # 参数S可以是数组(与f大小相同)或标量。
    # 如果S是数组，那么在所有种子点的坐标处必须为1，而在其他地方为0。
    # 如果S是标量，就将S定义为灰度值，在f 中，具有该灰度值的所有点都是种子。
    # T也可以是数组(与f大小相同)或标量。
    # 如果T是数组，那么对于f中的每个位置都应该包含阈值。
    # 如果T是标量，就将之定义为全局阈值。阈值用来测试图像中的像素与种子是否足够相似，或者是否是8连接的。
    f = im2double(f);
    if numel(S) ==1
        SI = f == S;
        S1 = S;
    else
        SI = bwmorph(S, 'shrink', Inf);
        S1 = f(SI);
    end
    TI = false(size(f));
    for K = 1:length(S1)
        seedVal = S1(K);
        S = abs(f - seedVal) <= T;
        TI = TI | S;
    end
    [g, NR] = bwlabel(imreconstruct(SI, TI));
end

d4395d2a21346b19c3524bc4dfa1b438.png

2. 区域分裂与合并

基本思路：类似于微分，即无穷分割，然后将分割后满足相似度准则的区域进行合并。 7d1b0460e929b604ec56f35e2ca6327d.png Matlab里用于图像分裂的方法是四叉树分解，函数是qtdecomp(f, thresh)，thresh是分裂的阈值，输出是一个稀疏矩阵。将该稀疏矩阵聚合用函数full()（full()：将稀疏矩阵转换为满矩阵）。使用四叉树分解图像，要先保证该图像为维度2的方形矩阵，矩阵宽度为2的倍数（16, 32, 64, 512 …）。 fb57cb13a4b9b09a9185b207ea86a530.png

计算机视觉
数字图像处理 学习笔记
最近更新
文章内容

数字图像处理学习笔记4

如何提高读papers的能力